最小二乗法とは
最小二乗法は、統計学においてデータの傾向を表す線を最も適切に引くための手法です。この手法は、観測されたデータとモデルとの間の差(誤差)の二乗和を最小化することにより、データの背後にある関係性を明らかにします。
背景と基本原理
最小二乗法は1805年にアドリアン=マリ・ルジャンドルによって初めて提案され、その後、カール・フリードリヒ・ガウスが独立して発展させました。主に、測定データから最も適合する関数を見つけ出すために使われています。
基本的に、最小二乗法は以下のステップで進行します:
- データセット内の各点と、推定したい関数(例えば直線や曲線)との間の垂直距離(誤差)を計算します。
- それらの誤差の二乗の合計を求めます。
- この合計が最小になるような関数のパラメータ(例えば直線の傾きと切片)を見つけます。
数学的表現
数学的には、最小二乗法は次のように表現されます。データセットが
(xi,yi)(i=1,2,...,n)で表されるとき、ある関数f(x)(例えば直線y=ax+b)に対して、誤差の二乗和
を最小にする
aとbを見つけることが目的です。
なぜ最小二乗法が重要か
最小二乗法は、科学や工学、経済学など多岐にわたる分野で広く利用されています。その理由は、データの傾向をシンプルかつ効率的に捉え、予測モデルやトレンド分析に利用できるからです。また、実験データから物理法則を導き出す際など、客観的で精度の高い方法として信頼されています。
最小二乗法をエクセルで求める方法
Microsoft Excelは、データ分析や統計処理に広く利用されるツールです。最小二乗法を使った回帰分析も、エクセルを使用することで簡単に実行できます。
流れ
- データの準備
まず、エクセルに分析したいデータを入力します。通常、一列に独立変数(時間、年齢など)、もう一列に従属変数(売上、身長など)を入力します。
- 回帰分析の実行
エクセルには、「データ分析」ツールが備わっており、それを使用して回帰分析を行います。データ分析ツールが表示されていない場合は、[ファイル] > [その他] > [オプション] > [アドイン] から「分析ツール」を追加する必要があります。
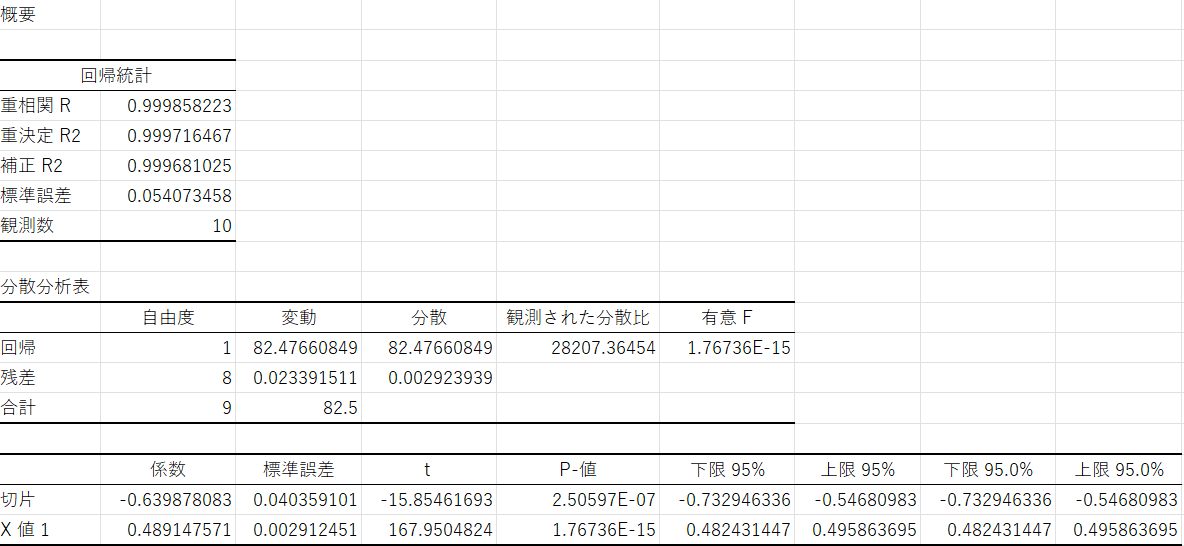
- 結果の解釈
回帰分析を実行すると、結果として回帰式や決定係数(R²)、係数の標準誤差などが表示されます。回帰式はデータの傾向を示し、決定係数はその傾向がデータにどれだけ適合しているかを表します。
回帰式の利用
回帰分析で得られる回帰式
y=ax+bでは、
aは変数の影響度を、
bは基本値を示します。この式を利用して、新しい独立変数の値に対する予測値を計算できます。
グラフを用いた視覚化
エクセルでは、分析結果をグラフとして表示し、データの傾向を直感的に把握できます。散布図に回帰線を追加することで、データと回帰線の関係を視覚的に確認できます。
LINEST関数を用いた最小二乗法
LINEST関数はエクセルで最小二乗法を用いた線形回帰を行うための関数です。より詳細な統計情報を得たい場合や、複数の独立変数を持つ回帰分析を行う場合に便利です。
LINEST関数の基本的な使い方
関数の入力
LINEST関数は、LINEST(known_y's, known_x's, [const], [stats])の形式で入力します。ここで、known_y'sは従属変数のセル範囲、known_x'sは独立変数のセル範囲、[const]は切片を計算に含めるかどうか(省略時はTRUE)、[stats]は追加の統計情報を出力するかどうか(省略時はFALSE)を指定します。
配列数式としての入力
LINEST関数は配列数式として入力する必要があります。関数を入力した後、Ctrl + Shift + Enterを押すと、関数が配列数式として認識されます。
結果の解釈
LINEST関数による出力は複数のセルにわたります。例えば、単純な線形回帰では、最初のセルに傾き、次のセルに切片が表示されます。[stats]をTRUEに設定すると、標準誤差や決定係数などの追加情報も得られます。
利点と活用
LINEST関数の利点は、その柔軟性にあります。複数の独立変数を持つ多変量回帰分析にも対応しているため、より複雑なデータ分析が可能です。また、追加の統計情報を通じて、分析の信頼性や精度をより深く理解できます。
最小二乗法のビジネスでの活用方法
最小二乗法はビジネスの様々な場面で有効に活用されています。データから有意義な情報を引き出し、意思決定をサポートする重要なツールとなり得ます。
市場分析と予測
最小二乗法は、市場のトレンド分析や需要予測に使われます。過去の販売データや消費者行動の分析を通じて、将来の市場動向や消費者の需要を予測することが可能です。企業はこの情報を基に、在庫管理、価格戦略、販売促進キャンペーンなどの計画を立てることができます。
事例
- 製品販売のトレンド分析
過去の販売データに基づいて、特定の製品の販売トレンドを把握し、需要の変動を予測します。 - 価格設定の最適化
販売価格と売上の関係を分析して、利益を最大化する最適な価格点を特定します。
リスク管理
リスク管理においても、最小二乗法が役立ちます。特に金融業界では、資産のリスクとリターンの関係を分析するために用いられます。ポートフォリオのリスクを最小限に抑えつつ、期待リターンを最大化する戦略を立案する際に重実されます。
事例
- 投資ポートフォリオの最適化
異なる資産クラス間のリスクとリターンの関係を分析し、リスクを管理しつつリターンを最大化するポートフォリオを構築します。
生産性の向上
生産プロセスや労働効率の分析にも最小二乗法が活用されます。生産データや労働時間に関するデータから、効率的な生産ラインの設計や作業プロセスの改善点を見つけ出すことができます。
事例
- 生産ラインの効率分析
生産量と必要な労働時間の関係を分析し、生産性の向上を目指すためのプロセス改善を行います。
まとめ
最小二乗法の理論的背景、エクセルを使用した具体的な分析手法、そしてビジネス現場での実践的な応用方法について解説しました。最小二乗法は、データの背後にある関係性を明らかにし、予測やトレンド分析を効率的に行うための強力なツールです。データ駆動型の意思決定が求められる現代において、最小二乗法はその汎用性と効果により、非常に価値の高い分析手法となっています。